Creating a Profitable Daily Fantasy Sports Strategy Using Genetic Algorithms and Free Data

Daily fantasy sports are legalized gaming contests that run in accordance with various professional sports leagues. In the contests, a contestant selects a lineup of players from a larger player pool and competes against other players. Several websites, like DraftKings and FanDuel, run daily fantasy contests and host various types of games. Two of the most common games are cash games, in which half of the pool doubles their money, and tournament games, where a small fraction of the pool gets paid in tiers.

Heated debate surrounds daily fantasy contests, where discourse occurs over whether the games are skill or luck based. Several papers have provided evidence that the games are skill based, and several states have legalized the contests [1]. Picking an optimal lineup is a multidimensional knapsack problem, and in this case, I tried my hand at implementing a genetic to pick optimal lineups.

The code for what follows can be found at my github, HERE.

Genetic algorithms have been used in different disciplines to solve a variety of combinatorial optimization problems, including the multidimensional knapsack. I considered several different genetic algorithm implementations and them implemented over 113 playing days in the 2019–2020 NBA season. I then compared the selected lineups to the average cash and tournament money lines needed to win in a respective contest on a given day. During the process I learned that the concept of applying a simple genetic algorithm to the process of selecting a lineup is a novel strategy that can provide exceptional results, quickly.

I also created a method to compare the created lineups to the average score needed to win a cash game contest and a tournament contest per day. The novel method of quantifying the genetic algorithm’s historical performance provided insight into how to tweak the algorithm to further maximize performance.

Picking Winners

After evidence supported that the games are skilled based, contestants have sought an edge over the larger field. As stated by DraftKings, 91% of players win a majority of the daily sports contests, pointing to the hypothesis that there is a method for selecting the best lineup. In the paper titled “Picking Winners in Daily Fantasy Sports Using Integer Programming”, researchers at MIT modified a “picking-winners” strategy to perform exceptionally well in tournament based games [2]. Their strategy involved linear optimization and creating sets of lineups with high variance in an attempt to maximize the possibility of picking a winning lineup in a tournament game… But their strategy involved entering 200 lineups a day. Entering 200 lineups a day could bankrupt the average daily fantasy player right off the bat.

The Infamous Multidimensional Knapsack Problem

Choosing a daily fantasy sports lineup is a multidimensional knapsack problem. A multidimensional knapsack problem is an NP-hard combinatorial optimization problem where multiple constraints are placed on decision variables [3]. I won’t bore you with the formulas, but finding an optimal solution for a multidimensional knapsack problem is exceptionally hard.

When applied to daily fantasy sports and in this case, NBA DraftKings contests were considered the proving ground. In a contest, a contestant must select 8 different players, each with a different position. DraftKings assigns a salary to each player, based on their past performance, and the total sum of the salaries in a lineup cannot exceed $50,000 [4]. A total of 2 or more teams must also be represented in each lineup. By placing multiple constraints on the problem, the odds of picking a well performing lineup are exceptionally low, even before adding performance of the players into the question.

Making The Case for a Genetic Algorithm

As I said before, finding a solution to multidimensional knapsack problem is HARD. In the case of daily fantasy sports, a lineup has to be optimized based on multiple constraints in order to produce a maximum number of fantasy points. In the past, it has been demonstrated that genetic algorithms can provide high quality solutions to multidimensional knapsack problems. Genetic algorithms can also offer solutions with minimal computational effort when compared with other optimization techniques. For a daily sports contestant, using a genetic algorithm that is fast, resource efficient, and converges to an optimal solution can provide an edge and help maximize profitability when compared to other contestants.

The Data

Collection

Several websites provide data geared toward daily fantasy sports contests. Since most websites offer paid services, it was important to find free, available data in order to maximize the profitability of the genetic algorithm strategy. Daily player data was collected from Daily Fantasy Nerd [5] and Daily Fantasy Fuel [6]. Both sites offered free, exportable .csv data. Both sites also allowed for the downloading of the previous day’s data, which was important for the construction of the historical performance backtesting model.

The data provided by the sites includes a variety of features. All of the data is also updated daily, which is important because a different set of players play each night. Some of the more important features included: player name, position, projected fantasy points, projected minutes, and projected value. Other features include a historical breakdown of a player’s average minutes, points, and fantasy points over the last 2 games, last 5 games, and season.

Since the genetic algorithm was run for every game of the season, quantifying the profitability of the algorithm was especially important. The RotoGrinder’s Results Database provides the values for the average cash game line and average tournament game line necessary for winning a contest [7]. The values of each day were collected and used to test the performance of each variation of the genetic algorithm.

Draftkings

DraftKings was used as the contest platform in this specific case, due to the amount of third-party data offered by various websites geared toward the DraftKings platform. DraftKings offers a variety of daily fantasy sports contests in all of the major sports. The NBA was chosen due to popularity, the amount of available data, and the frequency of games played. In theory, the genetic algorithm could be applied to any of the sports offered on the DraftKings platform.

The games offered by DraftKings fall into two major categories. Cash games and tournament games. Although there are different deviations of cash games, a cash game generally refers to a game, in which the prize money is paid to 50% of the contestants. In a $1 cash game contest, if a contestant is above the line needed to win, he is paid $1.80. For cash game contests, depending on the duration of play, a contestant must win 55.6% of the time in order to break even. With cash game contests, the average value needed to win is often lower than that of tournament games.

In tournament games, depending on the size of the contest and the entry fee, the prize money is usually paid to the top 23% of the players. The prize structure is tiered and the contestant with the top lineup wins a majority of the prize money. The break even percentage for tournament games is harder to quantify because the general payout structure varies. In order to quantify the winning threshold for tournament games, the RotoGrinder’s results database was used. Lines for placing in the top 3 and top 50 were calculated by selecting a sample and averaging the difference from the tournament baseline for the day. On average, to place in the top 3 a contestant needed to score 85 points above the line, and to place in the top 50, a contestant needed to score 58 points.

Correlation Matrix

After collecting data from the two different sources, the data was then merged and analyzed using Python and Pandas. Since the data contained a large amount of features, some unrelated, several features were merged. Features that were not strongly correlated were dropped to make managing the dataset easier. Figure 1 shows a correlation matrix of some of the features that aligned with the actual fantasy points a player scored on a given day.

The “Avg Proj” feature corresponds to average projected fantasy point values offered by each of the respected sites. Averaging the two values gave a higher respective correlation coefficient opposed to keeping the two values separate.

One of the main issues when dealing with the set of features was multicollinearity. The two sites formulate their projected point values using historical season data. The sites provided historical values for each of the players for the last game, the last 5 games, and the full season. By averaging each of the features, a higher correlation coefficient was obtained. Each of the feature formulas are listed on either the Daily Fantasy Fuel or the Daily Fantasy Nerd Websites. The only exception being, the “Proj Min Enhanced Feature”. In order to calculate the feature, the “Avg Proj” feature was divided by the “Avg Skewed Min” category and then multiplied by the player’s projected minutes for the given day.

The Genetic Algorithm

A several step process was used in designing a genetic algorithm for the problem of creating an optimal daily fantasy lineup. Taking into account the multiple constraints of the problem, construction of a genetic algorithm that produced valid lineups was of utmost importance.

For reference, the gene of the genetic algorithm was a player for a specific position. In a DraftKings NBA contest, a lineup consists of 1 point guard, 1 shooting guard, 1 small forward, 1 power forward, 1 center, 1 guard, 1 forward, and 1 player of any position. On one sample night, with 12 games and 24 teams playing, there are 4.75e16 possible combinations of different lineups without constraints. For the genetic algorithm, the chromosome was a valid lineup made up of the genes for each position. The population was a collection of valid lineups.

In order to initialize a population, players were bucketed by their respective position. A sample of 1 player was assigned to each position, and the lineup was fed to a function that validated the lineup was under the salary expectation of $50,000, the lineup contained players on two or more teams, and each player in the lineup was selected only once [8]. The random population generation algorithm then ran until enough validated lineups were created.

Attributes

The initial population size of the genetic algorithm was held constant for the duration of the run time. Several different values for the population size were taken into consideration. The population size influenced the run time of the algorithm, since finding valid lineups was essentially the multidimensional knapsack portion of the problem. A population size of 30 was considered optimal for this specific problem. Experimenting with values ranging from 10–100 offered multiple insights [9]. If the population size value was too low, the best players were not discovered due to the large size of the player pool and the randomness associated with the introduction of new players into the player pool. If the population size values was too large, increasing low value players that satisfied problem constraints were introduced into the created lineup set, creating noise. A population size of 30 allowed for balance between the two extremes.

In order to select children, the population was first sorted based on fitness value. The fittest selection was automatically introduced into the mating pool. Lineups 2–5, had a 75% chance of being selected. Lineups 5–10, had a 50% chance of being selected. Any lineup had a 33% chance of being selected. The roulette selection style was optimal for this specific problem, since it reduced the potential of selection for low value players.

The mutation strategy for this genetic algorithm application was not traditional. The algorithm was dependent on the introduction of new, higher-value players, in order to prevent finding a local optima too quickly. To introduce new players into the population, after performing crossover, all duplicated lineups were eliminated and replaced with completely random lineups.

Crossover

The process of creating children was the biggest bottleneck for the genetic algorithm implementation. If two parents were used for crossover, there existed a high possibility that the two parents were the only valid lineups that could be produced. Randomly generating a valid child from the set of parents if no other possible valid child existed presented a major inefficiency in creating the next generation.

Multi-point crossover was essential for this case, since each player could only be swapped with other players from the same position, due to constraints. To combat the valid parent problem, a mating pool was constructed, using all of the selected parents. The generation of children was similar to the process of initializing the random population, with the exception of the amount of players represented. By using the selected parents, 10 children were created more efficiently than using two selected parents. Through testing, the method of using a mating pool was non negligible in terms of the fitness of the final population. Using the mating pool provided an optimization in terms of speed.

Fitness Function

In order to be considered performant, the genetic algorithm needed to not only find lineups that met the constraints, but also lineups that performed better than other players. Optimal lineups, lineups that would achieve a higher score than other lineups were difficult to find, but the process of finding the lineups directly related to the implementation of the fitness function.

Several different fitness functions were juxtaposed for the genetic algorithm. Since the “Avg Proj” feature was highly correlated with the actual fantasy points scored value, the first fitness function was just the sum of the projection values for each of the players in a lineup. Using the singular feature was considered the benchmark for the experiment.

Since the rest of the features were linearly correlated with the actual points scored value, the next step in creating a fitness function was to use a linear regression model aiming to create a prediction value that was more valuable than using the projected point value alone. In order to assure the integrity of the model, predictions were made on unseen data, after each training day, the player instances were appended to the larger historical data set. As the number of playing days increased, the size of the training data set also increased.

Finally, for the third fitness function type, an elastic net model was used. Elastic net regression uses regularization, to influence the variance and bias represented by the model. For each playing day, a GridCV search was run to determine the optimal hyperparameters of the elastic net model. In the following section the performance of each of the fitness functions is analyzed.

Finally… Performance

The implementation of the genetic algorithm was tweaked several times in order to find an optimal solution. The following section describes how profitability was established, highlights the different implementation of the genetic algorithm, and shows the performance of the different implementations of the genetic algorithm.

Establishing Profitability

In order to quantify the performance of the genetic algorithm, a system for establishing profitability needed to be created. No current backtesting model for daily fantasy sports currently exists. In some contests, contestants are limited to entering one line, while in others, contestants can submit up to 200 different lineups.

Data was collected for 113 playing days of the 2018–2019 NBA season. The RotoGrinder’s results database provides the average cash line and average tournament line needed to be in the money for the collection of contests per day. As previously mentioned, to be profitable in cash games, a contestant needs to win 55.6% percent of the time, due to winners being paid out $1.80 from their $1 entry fee [10].

For tournament games, the payout structure differs. A smaller size of contestants win payout money and the payout is in tiers based on ranking compared to other contestants. In order to establish profitability for tournament games, a sample of 10 NBA games were considered. For each of the games, the minimum point value needed to place in the top 3 and top 50 was compared to the tournament cash line for the given day. The average difference was used to qualify lineups that would place in the top 3 and top 50 for a given day. The minimum payout for placing top 3 in the largest contest for a $1 entry equates to a payout of $500, and the minimum payout for finishing in the top 50 equates to a payout of $25. The returns for playing tournament games are exponentially higher than cash games, but the average lines are often higher than the cash lines for a given day.

In order to quantify the performance of each genetic algorithm, the sum of actual fantasy point values of the players in each lineup were compared to the cash and tournament lines for each day. A top 3 finish was counted if the sum of the point values exceeded the tournament line by 85 points, and a top 50 finish was counted if the sum exceeded the tournament line by 58 points. For each of the game days, entry fees of $1 were considered.

Benchmarking

In order to ensure that a genetic algorithm did in fact provide optimal lineups, each of the models were compared against a sample of 10 randomly generated lineups per day. The 10 lineups were constructed using the same function that initialized the initial genetic algorithm population.

In order to compare the different fitness functions, the fitness function based solely on the sum of the projected fantasy point values was used as a benchmark.

Comparison of Genetic Algorithm Models

The elimination of duplicate lineups and the introduction of random lineups into each population betrothed noise and the final population. Noise of some form was necessary in the genetic algorithm in order to introduce new high value players and in order to prevent the algorithm from finding a local optima too early. Since the noise was present in the final population, only a selection of the final population was considered as “most fit”. In practice, limiting the amount of entries into a daily fantasy sports contest conserves bank roll and helps optimize profitability.

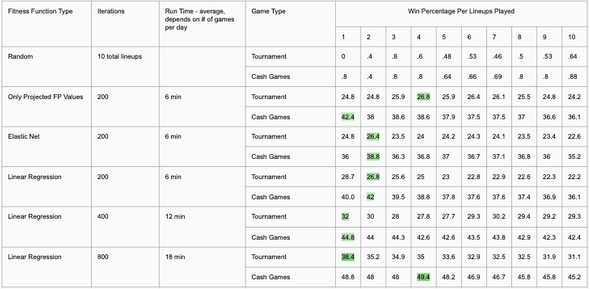
The table below shows the comparison of each of the different models against the benchmarks. The win percentage per number of lineups played column corresponds to the number of lineups entered into a contest for a given day. If 1 lineup is entered, the sum of the actual points of the fittest lineup is compared to the average lines for the day. If 10 lineups are entered, the 10 fittest lineups are compared to the average lines per day. The average runtime, varied by the amount of players present for a given day, is included. Also, the number of iterations before terminating is present. Different forms of termination criteria were experimented with, but running the algorithm for a fixed number of generations provided the best results when compared to the benchmarks.

The randomly generated lineups had a sub 1% chance of winning any type of game for the duration of the season. The benchmark of using only the sum of projected fantasy points performed best in cash games when 4 lineups were entered, netting a winning percentage of 26.8%. The highest cash game performance was 49.4%, attributed to the implementation of linear regression as the fitness function, running 800 generations with 4 lineups at play. The same implementation performed best again in tournament games. With only one lineup in play, the implementation won 38.4% of the time.

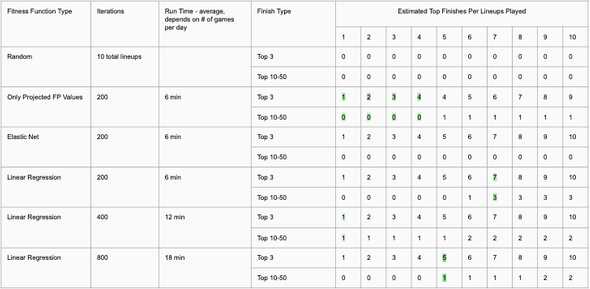
Although none of the implementations met the profitability criteria necessary for cash games. The concept of using a genetic algorithm to pick an optimal daily fantasy lineup is not to be discounted. In tournament play, the implementations all perform decently. The table below shows the projected placement in tournament games for each of the strategies.

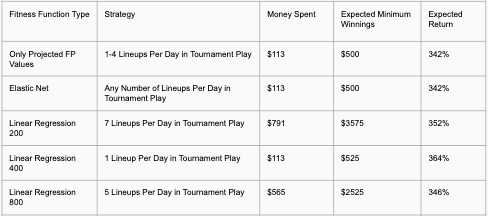
Outside of each of the randomly generated lineups, the strategies were able to find tournament winners over the course of the season. One takeaway is that as the number of lineups entered expands, the number of top 3 winners also expands, this can be attributed to the fact that most of the top lineups contain similar players. The linear regression model running for 400 generations performed best, providing a top 3 winner and a top 50 winner on a single entry each day over the course of the season. Table 3 highlights the minimum expected returns from playing each implementation’s most profitable strategy.

Playing tournament games with each of the respective strategies banks on high placement in one of the contests over the course of the season. Since the linear regression model running for 400 generations found a top 3 winner and a top 50 winner on only one entry per day, it is considered the most profitable implementation.

Conclusion

Using a genetic algorithm for picking daily fantasy sports lineups can be considered an effective strategy. The previous experiment, implies a contestant having no knowledge about the NBA. The experiment also only uses projection and historical data values from two free fantasy sports sites. By engineering different features or using paid services, a contestant may be able to gain a competitive edge.

A major inefficiency in the algorithm’s implementation is the amount of noise that must be allowed in order to find high value players for a given day. By shrinking the player pool, a contestant could eliminate some of the noise of low value players and create a more optimal strategy.

The previous experiment demonstrates that genetic algorithms can be used to construct near optimal lineups. By implementing the algorithm for another sport, where projection point values have a lower variance from actual point values, a contestant might see better results. In conclusion, this experiment serves as a proposition of the value of using genetic algorithms to solve multidimensional knapsack problems.

If you made it this far… thank you for reading and HERE is the link to the github again. Try it on a different sport, the results may impress you!

References

1. Getty, Daniel, Hao Li, Masayuki Yano, Charles Gao, and A. E. Hosoi. “Luck and the Law: Quantifying Chance in Fantasy Sports and Other Contests.” SIAM Review 60, no. 4 (January 2018): 869–887. © 2018 SIAM.
2. Hunter, D. Scott, Juan Pablo Vielma and Tauhid Zaman. “Picking Winners in Daily Fantasy Sports Using Integer Programming.” (April 2016).
3. M. Berberler, A. Guler, and U. Nurıyev, “A Genetic Algorithm to Solve the Multidimensional Knapsack Problem,” Mathematical and Computational Applications, vol. 18, no. 3, pp. 486–494, Jan. 2013.
4. DraftKings. DraftKings. http://draftkings.com, February 2020.
5. DailyFantasyNerd. Daily fantasy nerd. http://dailyfantasynerd.com, February 2020.
6. DailyFantasyFuel. Daily fantasy fuel. http://dailyfantasyfuel.com, February 2020.
7. Rotogrinders. Rotogrinders. https://rotogrinders.com/, February 2020.
8. J. Nederlof, “Genetic Algorithm for DFS,” Medium, 22-Feb-2019. [Online]. Available: https://medium.com/@jarvisnederlof/building-a-genetic-algorithm-in-python-for-daily-fantasy-sports-9f497d378e34. [Accessed: 30-Feb-2020].
9. C. Shyalika, “Population Initialization in Genetic Algorithms,” Medium, 28-Jan-2019. [Online]. Available: https://medium.com/datadriveninvestor/population-initialization-in-genetic-algorithms-ddb037da6773. [Accessed: 1-Mar-2020].
10. D. Y. Wohn, E. J. Freeman, and K. J. Quehl, “A Game of Research,” Proceedings of the Annual Symposium on Computer-Human Interaction in Play, 2017.

• ← Leveraging Machine Learning to Predict Stock Prices
• Save Yourself from a Stock Market Crash with this Simple, Free Strategy →